2000-01-31[n年前へ]
■落ちゆくエレベーターの中…で悩みます? 
無重力の理想と現実(仮)
今日もまた「ちゃろん日記(仮)」を読みに行くと、何とも面白い話があった。
である。この「ちゃろん日記(仮)」は「疑問とそこに隠れている真実を見つけだす感覚」に満ち溢れている、と私は思うのである。面白すぎである。さて、今回の話は、エンパイアステートビルでエレベーターが落ちたっていうけど、落ちていくエレベーターの中の人は
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
「ほんとう〜にそうか? ほんとう〜にそうか?」
こういういかにも教科書に載っていそうな話には、時として落とし穴がある。教科書に書いてあるのは理想的で単純化した場合の結果である。それを鵜呑みにすると間違えてしまうことになる。極端に言えば、教科書に書いてあるような理想的な状態はほとんど存在しないので、教科書に書いてあるような現象はそうそう再現しない、ということになる。
ピサの斜塔から「落下の実験」を行ったのはガリレオ・ガリレイであると思っていると間違いである、というのは少し違う例になってしまうか。
久しぶりに思い出したが、私の所属していた研究室では重力測定は大きな柱であった。そして、確か大学院の入試問題の内の一題は、まさに
「落ちていくエレベーターの中の人達に働く力を精密に論ぜよ」であった(簡単に大雑把に言えば)。私はちゃんとこの問題を解けた覚えがない。いや、はっきり言えばずいぶん悩んだ覚えしかない。ってことはいまいち解けなかったのだろう。なので、「落ちていくエレベーターの中の人達は無重力状態である」と聞くと、「ほんとう〜にそうか? ほんとう〜にそうか?」と歌いたくなる。
研究室関連では、絶対重力測定を行う研究をする人達もいたわけである。絶対重力(加速度)測定は自由落下する物体の運動を測定して、重力加速度を測定するわけであるが、そう簡単に物体は自由落下してくれないのである。簡単な実験で物体を自由落下させて重力加速度を測定してみるとわかるが、大雑把な実験(自分の家ですぐできる程度の)では一桁ちょいの精度しか出ない。一桁ちょいの精度しかでないということは、(例えば)体重が10%弱程度になったように感じるかもしれないが、それは無重力ではない。体重が60kgの人であれば、6kgも感じてしまうのである。(雑な話だが。)
空気中を落ちてくる雨だってそうだ。もし、雨が自由落下を続けていたらものすごいスピードになって、雨に打たれるのは命がけになってしまう。しかし、実際にはそんなことはない。空気抵抗で速度は飽和してしまい、自由落下状態ではないからである。
さて、本題である。果たして、
例えば、
- 若井研究室の研究概要
- http://mech.gifu-u.ac.jp/~wakailab/research/Basic/base_h.html
北海道の上砂川町にある施設(JAMIC)で、490m落下させることにより、10秒の無重量環境が得られます。落下中は空気抵抗を受けるので、落下カプセルを二重構造にし、空気抵抗を無視できるように工夫してあります。と、記述されているように、実際には工夫をこらさなければ無重力状態は実現できないのである。絶対重力系などでも空気抵抗を無視するために、投げ上げて往復運動を測定するなどの工夫がいるのである。
と、言葉だけで書いてもしょうがないので、適当な計算でもしてみる。いや、もちろん、実験をするのが良いわけであるが、面倒だし…
まずはエレベーターには、
- 何の抵抗も働かない
- 空気抵抗とワイヤーの抵抗が働く
そして、エレベーターの中の人には空気抵抗は働かないとした。エレベーターの中の空気と人の速度差はほとんどないからである。また、エレベーターは人よりもはるかに重く、人の重さはエレベーターの運動に何の影響も及ぼさないと近似した。
その計算の結果を以下に示す。これが落ちていくエレベーターの軌跡である。抵抗のない場合が(赤)で抵抗のある場合が(青)である。エレベーターが落ち始めてから30秒後までの軌跡である。
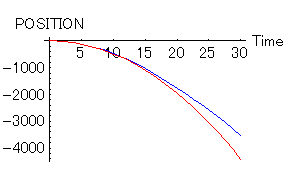 |
理想的な場合(赤)に比べて、抵抗のある場合(青)の落ち具合が鈍っているのがわかると思う。それでは、もっと時間が経った場合はどうだろうか?それを次に示す。エレベーターが落ち始めて300秒後までの軌跡である。つまり、五分間もこのエレベーターは落ち続けているのである。落ちた距離は理想的な場合で40kmの深さに達している。すごいエレベーターである。こんなに落ち続けていると、すでに重力加速度が一定とは言っていられなくなる。
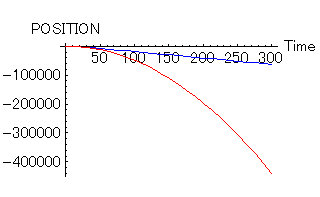 |
ここまでくると、抵抗のない場合(赤)と抵抗のある場合(青)では全然違う軌跡になっている。抵抗のない場合(赤)では放物線そのものであるが、抵抗のある場合(青)では一定の速度になっている。
それでは、エレベーターがこのような状態になった時の、エレベーターの中の人に働く加速度(と実際の加速度の差分)を示してみる。これを見れば、落ちていくエレベーターの中の人が無重力状態であるかどうかがわかる。まずは、300秒後までの変化を見てみる。
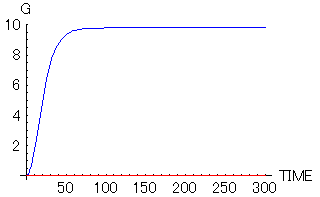 |
理想的な場合(赤)はずっとゼロすなわち無重力状態であるが、抵抗のある場合(青)は無重力状態は最初だけで、50秒後位には通常の状態に戻ってしまっている。最初の部分をもう少し拡大してみる。次に示すのは、3秒後までの落ちていくエレベーターの中の人に働く重力加速度(と実際の加速度の差分)である。
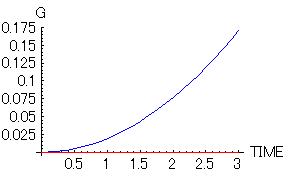 |
これを見ると、あっという間に人は無重力状態ではなくなっているのがわかると思う。
というわけで、先の三つの選択肢、
- 床に張り付く
- 天井に張り付く
- 宙に浮かぶ
先日みたニュースのエレベーター落下実験の中で、中にいた男性リポーターが、落下しながら「ひぃ?」とアオ向けになった状態で床にハリ付いていたからなのです。という実際の現象が正しいのである(いや、もちろん状況はかなり異なるが)。「頭の中だけ」で考えたことというのは大抵の場合間違ってしまう。(もちろん、今回の「できるかな?」の話もその例外ではない)
そして、その後に、
ありはきっと、速度がそこまで充分でなかったのと、もしやのトキのために、男性リポーターに安全な姿勢をとらせていたタメだと思われます。とあるが、実際問題として「速度がそこまで充分」になることは未来永劫ないわけである。だから、(私の中では)エレベーターの中の男性リポーター氏は床から浮かぶことはないのである。
こういうのは、結局考える人の数だけ答えがあるのだと思う。もし、その内のどれが真実に一番近いかどうか知りたければ、実験すれば良いだけの話だし。
2000-10-29[n年前へ]
■「しょんべん小僧」の物理学 
あともう一歩、前に出ろ
以前、- スクール水着の秘密 - 腹の部分のデカイ穴 流体力学入門編2 - (2000.08.24)
「男性にはよくある風景だけれど、女性にとっては未知のミステリアスゾーン」といってもたくさんあると思うが「男子トイレ」というものだって、女性にとっては未知のミステリアスゾーンだろう。
次の絵はよくある男子トイレの一風景だ。便器前のポジションに立つとどうしても目に入る位置にこんな内容を書いたチラシが張ってあることが多い。
「ちょっと待て、あともう一歩前に出ろ。」
 |
もし、その張り紙がなかった場合にはどうなるだろうか?その場合には、下の絵のような事故が発生してしまうのである。実際のところ、ほとんどの公衆便所で見かける風景だ。
 |
そう、便器にロックオンして放水をしたハズなのに、何故かターゲットである便器まで「小便」が届かずに便器下を汚してしまうのである。実にマズイ事態ではあるがよく見かける風景でもある。便器内を狙ったハズの小便が残念ながら目標地点まで辿り着かなかった場合に起きる悲劇である。
もちろん、どんなに飛距離が小さくても、すなわち小便が放水銃の先から真下に垂れてしまった場合でも、便器の顎の上から放水作業を行っていれば何の問題もないわけだ。しかし、世の中の男性達は何故か遠くから狙いたがるのである。先程の、「ちょっと待て、あともう一歩前に出ろ。」という張り紙ではないが、もう一歩前に出て便器の顎の上から放水作業を行いさえすれば良いのではあるが、何故か漢(ここではあえて、漢と書いてオトコと読むことにしよう)達はそれができないのである。
さて、この現象には別に公衆便所でなくても発生するわけで、どこのトイレでも便器の下を汚してしまうことになる。そのため、家庭によっては妻から
はるか古の昔から「男らしさ」のひとつが「立ち小便」でなかったか?、そして「立ち小便」は「男らしさ」の最後の砦ではないのか?という気も私は少しだけしたりするのだが、便器周りを汚しまくる現実の前ではそんな「男らしさ」は2000円札よりも価値がないのである。2000円札ならば喜んで受け取ってくれる人もいるだろうが、便器の下に落ちようとする「小便」は誰も受け取ってくれない。いや、実際のところ小便を喜んで受け取ってくれる人もいるのかもしれないが、少なくともそんな人の数は2000円札を喜んで受け取る人の数よりはきっと少ないだろうと思うのである。
そしてさらに、「男らしさ」が「立ち小便」なら、そんなものイラナイと言われてしまいそうな気もするし、「立ち小便」が「男らしさ」の最後の砦か!?と言われてしまいそうな気も強くするので、ここらへんについての社会学的な考察は追求しないでおこう。
それでも、私は世の中の虐げられている「しょんべん小僧」達のため、そして「男らしさ」の最後の砦を守るために、男子トイレの「しょんべん小僧」達がどうしたら、放水ミスをしないかを物理的に考えてみることにしたい、と思うのである。
さて、便器まで小便が届かないという「放水ミス」はどのようにすれば防ぐことができるだろうか?小便の飛距離を小さくしないためにはどのようにしたら良いだろうか?そのためには、まず小便の飛距離がどのようにして決まるのかを考えなければならないだろう。
下のちょっとリアルな「しょんべん小僧」の放水作業ではないが、小便の軌跡はきれいな放物線を描く。
 |
すなわち、空気抵抗などは無視した場合のピストルの弾と同じく
- 銃筒の先端を出るときの初速度
- 銃筒の角度
銃筒の先端を出るときの初速度 = V0と表すと、小便の飛距離は
銃筒の角度 =θ
a V0^2 Sin[2θ] (aは定数)と表される。この式を見ればθ = 1/2 rad.の時にSin[2θ]が1になるので一目瞭然であるし、また感覚的にも自然であるが、銃筒の角度の方は上向き45度の角度に向けるときに小便の飛距離は最大になる。一方、初速度V0の方は速ければ速いほど、小便の飛距離は伸びる。
それを示したのが、次の図である。「小便の銃筒の先端を出るときの初速度と銃筒の角度を変えた時の小便の飛距離」を示したものだ。
 |
すると、便器まで小便が届かないという「放水ミス」すなわち、小便の飛距離を小さくしないためには、銃筒の角度を大きくしすぎたり、小さくしすぎたりしないという知見が得られるわけであるが、そんなことは当たり前だ。誰もトイレで銃筒を真上に向けたり、真下に向けたりはしないのである。先のちょっとリアルな「しょんべん小僧」ではないが、手で放水銃を支持している限り何の問題も無いのである。
つまり、便器まで小便が届かないという「放水ミス」はほとんどの場合「放水銃の角度」のせいではないのである。つまり、「銃筒の先端を出るときの初速度」が問題だったと考えるのが自然である。
それでは、「銃筒の先端を出るときの初速度」はどのようにして決まっているのだろうか?それを大雑把に考えてみたのが次の図である。腹筋で膀胱に圧力Pをかけて、銃筒の先端から小便を初速度V0で放水作業を行うのである。
 |
ところで、上の絵でポンプとして表した膀胱に圧力Pをかけた場合には、膀胱からb P (bは比例定数)と表せる量の小便が銃筒に送り込まれるものとしよう。その場合、その量の小便が銃筒の先端から単位時間に出るわけであるから、銃筒の先端の口径をAとすれば、
V0 = b P /Aと表すことができる。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのである。
さて、いくら腹筋が強い人であっても腹筋をいきなり締め付けることはできない。つまり、腹筋で膀胱を締め付ける圧力Pというものは徐々に大きくなるのである。
すると一見、「銃筒の先端を出るときの初速度V0」も0から徐々に大きくなる、すなわち、放水作業を開始した最初の瞬間は「銃筒の先端を出るときの初速度V0」= 0であって、小便の飛距離も0である、つまり、便器まで小便が届かないという「放水ミス」が必ず起きるかというと、実はそういうわけではない。
ポンプである膀胱から銃筒の先端までは、ある程度の長さがある。もちろん、その長さは一定ではないのだが、とにかくある程度の長さがある。そのため、小便が銃筒の先端から出る瞬間には、ポンプである膀胱にかかっている圧力Pは0ではないのである。すなわち、膀胱から銃筒の先端まである程度の長さがありさえすれば、「銃筒の先端を出るときの初速度V0」は結構大きくすることができるのだ。もちろん、腹筋を鍛えて、腹筋に急激に力を掛けることができれば、その効果はさらに上がることは言うまでもない。
だとしたら、一般的に便器まで小便が届かないという「放水ミス」は一体何時起きるのであろうか?それは、「銃筒の先端を出るときの初速度V0」を決める膀胱にかかる圧力Pが低下し、なおかつ最初の瞬間と違い「膀胱から銃筒の先端までの長さ」を有効に活用できない、放水作業を終える瞬間である。飛行機でも着陸が一番難しいというが、この放水作業もやはり放水作業を終える瞬間が一番難しいのである。そのため、多くの場合小便達は便器内への着陸に失敗し、便器の下を汚してしまうのである。
しかし、私は「男らしさ」の記念物でもある「立ちしょうべん」を守るために、一つの解決策を考えついたのである。「男らしさ」の最後の砦を守る技術を提唱したいのである。すなわち、「銃筒の先端を出るときの初速度V0」は腹筋で膀胱を締め付ける圧力Pに比例し、銃筒の先端の口径Aに反比例するのであるから、放水作業のラストに膀胱を締め付ける圧力Pが小さくなった、あるいは、膀胱を締め付ける圧力Pを有効に膀胱からの排水に変換できない排水作業のラストにおいて、銃筒の先端の口径Aを小さくしてやればよいのである。そうすれば、「銃筒の先端を出るときの初速度V0」は「銃筒の先端の口径A」に反比例するのであるから、膀胱から出てくる小便の量が低下しても、「銃筒の先端を出るときの初速度V0」を0にならないように維持することができるのである。これにより、放水ミスを防ぐことができるハズなのである。
さて、私は「男らしさ」の最後の砦である「立ちしょうべん」を守るために、このような技術を考えてみたわけであるが、この技術の実証作業は行っていない。果たして、「銃筒の先端の口径A」を自分の意識で小さくすることができるか!?というところに大きな問題点があるような気もするのであるが、それは「男の意地」で克服できると私は信じている。外部から制御するって手もあるのだし。って何の手の話だ、全く。
2001-05-20[n年前へ]
■オッパイ星人の力学 あなたのオッパイ星人度 編 
擬似オッパイに関するhiraxの関係式
オッパイ星人シリーズも第六回である。いつの間にか、「片手」で数えられる回数を超えてしまった。前回の話では、大仏が差し出す「片手」も実は擬似オッパイの感触を楽しんでるのかもしれない、という結論だった。今回はそんな「時速60キロの風圧はおっぱいの感触か?」という問題の続きを少し違うアプローチで考えてみたい。そして、そもそもの出発点「時速60キロの風圧はおっぱいの感触か?」を考え直すとともに、前回の目的「そんな危ない擬似オッパイではなくて、青少年のためにもっと安全な疑似おっぱいを探す」ということについても考え直してみたいと思う。
まずは、簡単な「あらすじ」を先に書いておこう。
なんでも、テレビ番組の「めちゃめちゃイケてる!」の中で「時速60キロの風圧はオッパイの感触である」と言っていたらしい。そしてまた、人間そして愛について日夜取り組んでいる「性と愛研究所」の「おっぱいの感触と風圧に関する考察」中で、「時速60kmでは全然オッパイの感触ではなくて、ちょうど時速100kmを境に急にオッパイの感触を感じます。」というメールが紹介され、擬似オッパイの感触を受けるのは時速100km以上だと結論づけられている。前回、私自身も東名高速で出勤途中に確認してみた感じでは「時速100km/h」以上が妥当に思われた… と、その時は思われたのだが、先日またもや東名高速で出勤途中にふと実験し直してみると何か違うのである。「時速100km/h」では風圧が強すぎるのだ。「時速60km/h」でも「何やら十分イケてる感じ」に思えたのである。「オヤ?これは一体どういうことだ?」と私は疑問に思うと同時に、そういえば「時速60キロの風圧はオッパイの感触か?」という問題を長いこと放り出していたなぁ、久しぶりにアレをやってみるかぁ(遠い目)と思い筆を取る次第である。
この前、
では車の窓から突き出した掌の指の形状を考えながら、その指の周りの空気流の計算してみた。もちろん、こういった形状的なアプローチも必要なのであるが、原理的なものを考えようとした場合にはそれはちょっと応用編すぎる。今回は単純な近似則を使って、「風圧はどの程度の大きさなのか?」「そして、その風圧の大きさはどの程度のオッパイの大きさなのか?」という風に考えていくことにしよう。 まずは、下に示すのが単純な手と複雑な手だ。左が私の掌で、右が私の目標ドラえもんの掌である。私の掌は結構複雑な形状をしている。それに対して、ドラえもんの掌の方は極めて単純、球そのものである。もう、ツルツルの球そのまんまなのである。
 |  |
複雑な私の掌の方は、さすがに複雑というだけあって掌の周りの空気流なんかを計算しようとすると、結構それは複雑だ。何しろ、前回は簡単な空気流の計算を行っただけでも出力ファイルは1ファイル当たり1Gバイト程になった位である。
しかし、右のようなドラえもんの単純な掌の場合はどうだろう?ツルツルの球そのまんまの掌は空気流により、どんな力を受けるだろうか?こちらの場合も計算は複雑なのだろうか?
実は、このツルツルの球そのまんまの掌の場合はそれほど計算は難しくないのである。一般的に、速度vで動く半径rの球が受ける「空気の粘性により生じる抵抗力」はストークスの法則により、
- 粘性抵抗
と表されることが知られている。ここで、ηは空気の粘性率である。標準状態の空気ではη=1.82x10^-5(kg/ms)である。式を眺めれば判るように、この粘性抵抗は球が動く速度vに比例した大きさになる。
どうして粘性によって抵抗力が生じるかはまた別の回で考えることとして、とりあえず掌が受ける抵抗にはもうひとつ大きなものがある。それが、一般的に「慣性抵抗」と言われるものである。こちらの方は、掌が静止している空気の「いわゆる」速度を変化させることによる抗力であり、半径rの球に対しては近似的に、
- 慣性抵抗
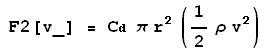
ツルツルの球形状の掌の半径rは、私の掌を握りしめた時の大きさを参考にして0.1(m)としてみた。もちろん、このサイズではちょっとでかすぎるわけだが、実際の掌の形状はもっと複雑で空気抵抗が大きいことを考慮して、実際の掌の受ける力に近づけるために大きめに設定してみた。
さて、掌を窓から出す車の速度を時速60km/hとか100km/hとかいった辺りで
という条件下で計算を行うと、粘性抵抗よりも慣性抵抗の方がはるかに大きく、掌の受ける力はほとんど慣性抵抗である。試しに、これらの数値を使って窓から出した(単純な)掌が受ける力を計算してみたのが次のグラフである。このグラフを見れば、窓から出した掌が受ける力が車の速度の二乗に比例していることが判ると思う。なお、ここで掌が受ける力の単位は(g重)に換算したものである。オッパイ星人の力学を考えるときの単位はkgでなくて、gの方が使いやすいのである。
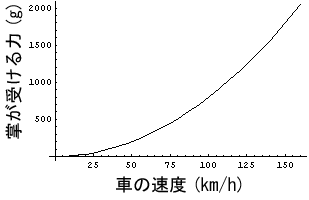 |
まずは、このグラフを見ると時速60kmでは掌に300g重位の力を受けていることが判るし、それが時速100km程度になれば大幅にその力は増えて800g重程度になる。掌にズシっと力を受けるわけである。
さて、掌が受ける力が判ってしまえば、こっちのものだ。何しろ、こっちには懐かしのオッパイ星人の力学シリーズ第一回
で計算した「胸のカップ数とオッパイ一個あたりの重さ(g)」(もちろん、この「オッパイ一個あたりの重さ」の値はどうにもおかしいところがたくさんあるのだが、そこはそれ女性の神秘(トリック?)なのである)がある。これを使って、窓から出した掌が受ける力を比較してみることにしよう。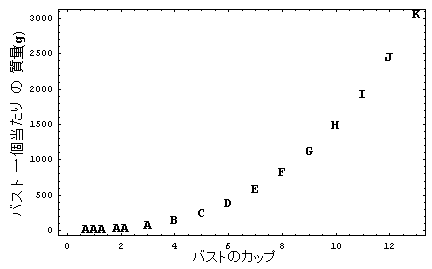 |
この「オッパイ一個を持ち上げるときの掌が受ける重さの感覚」を「窓から出した掌が受ける力」と比較してみる。すると、窓から出した掌が感じる擬似オッパイがどの程度の大きさであるかが判ることになる。極めてバーチャルな擬似オッパイのカップサイズが判るわけである。
というわけで、下に示したグラフが
- 窓から出した掌が受ける力 ( g重換算 )
- 胸のカップ数とオッパイ一個あたりの重さ(g)
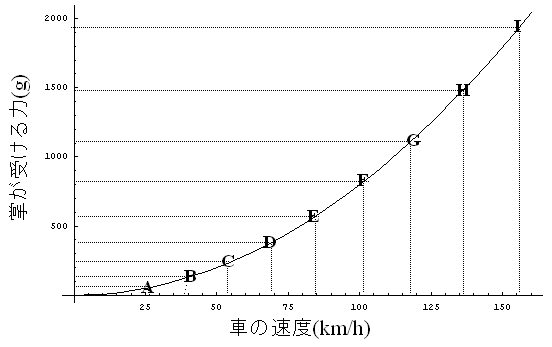 |
おやっ、なかなか良い対応が見られるではないか!時速60km/hというと、C〜Dカップ位のオッパイの感覚で、時速100km/hだとFカップ位である。時速30kmでもA〜Bカップ位のオッパイを持ち上げる位の力を窓から出した掌は受けていることになる。
ということは、各人の「擬似オッパイを感じる速度」が判れば、「その人が願うオッパイのサイズ」が判るのではないだろうか?そして、もし「その人の願うオッパイのサイズ」が結構大きければ、それはすなわちオッパイ星人度が高いということになるし、「その人の願うオッパイのサイズ」が小さければオッパイ星人度が低いということが判るわけである。
例えば、先の「時速60kmでは全然オッパイの感触ではなくて、ちょうど時速100kmを境に急にオッパイの感触を感じます。」というメールの書き主の思うオッパイのサイズは何とFカップである、ということが判るわけだ。実際のところ、何が標準かどうかは判らないが、Fカップというのはかなりな巨乳に思えることであるし、このメールの書き手はとてもオッパイ星人度が高い、ということになる。
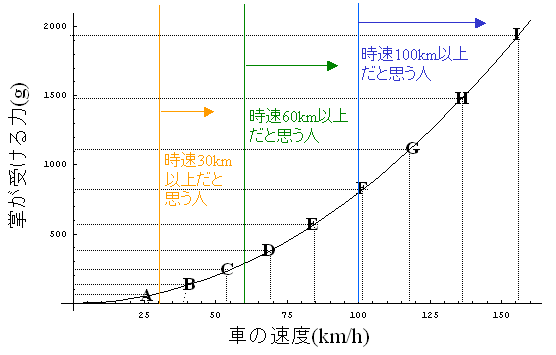 |
ぜひ、あなたもこのグラフを片手に、走る車の窓から手を突き出し、掌に受ける擬似オッパイの感覚を確かめて欲しい、と思う。そして、「擬似オッパイの適正速度」を頼りにあなたのオッパイ星人度をチェックして欲しいのである。そして、その結果を是非私(jun@hirax.net)まで知らせて頂けたら幸いである。
さて、前回「安全な擬似オッパイ」を探すべく考察をしてみたわけだが、実は考え直すべきは「人の願うオッパイのサイズ」であったのかもしれない。Eカップ巨乳を願うから時速100km/hが必要だったのであって、Cカップで満足すれば、時速60km/hで十分だったのである。そして、Aカップを願うならば、スクーターでもオッケーの時速30km/hでこと足りるのである。そう、実は車の窓から掌を突き出す擬似オッパイはとても安全なものだったのである。その本来安全な「車の窓から掌を突き出す擬似オッパイ」を危険たらしめていたのは、「高すぎるオッパイ星人度」だったのである。
というわけで、交通安全、そして世界平和へ通じる道は、実はオッパイ星人度を低くしていくことにあるのかもしれない、と思う今日この頃なのであった。
2002-05-19[n年前へ]
■風上に向かう「しょんべん小僧」 
「しょんべん小僧」の物理学 逆風編
近所の海辺で、不思議なお堂を見つけた。迷路のような曲がりくねった裏小路を抜けて行くと、小高く鋭い丘があって、その上に小さな八幡宮が建っている。そして、その丘(というより小高い岩)の中腹には小さな不動堂が建っている。かつては不動堂がその丘のヌシであったらしく、その丘は不動岩と名付けられている。とにかく、本当に小さいけれど、とても不思議な空間なのである。そして、その不動岩のてっぺんで潮風に吹かれて体が冷えたワタシは、バチ当たりにも立ちションをしてしまったのだ。
恥ずかしい話ではあるが、ワタシはトイレが近い。長〜い重要な会議中、カリカリと鉛筆の音が響く試験中、ビアグラスがぶつかる音が溢れる居酒屋で、あらゆる時、あらゆる場所でソレをもよおすワタシは、あらゆる場所でソレをする。もうそれは散歩中の犬並といっても良い位にソレをしまくるのである。
思い起こせば、観光バスで首都高速を走っているときに、いつものようにソレをもよおしたワタシは、観光バスに満載された同級生達(もちろん男女共に満載である)の視線を背中に浴びまくりつつ、首都高速の道路沿いで立ちションにいそしんだことすらあるくらいだ。そして、さらに真相を書いてしまえば、その時にはあまりの背中に降り注ぐ視線のイタさに(膀胱に押し寄せる強風波浪に関わらず)ろくに放水活動ができなかったことも、今となっては懐かしくも哀しい思い出なのである。
海辺の不動岩の上で潮風に吹かれながら、そんな「立ちしょんべん」にまつわるエトセトラを思い出したワタシは、久々に「しょんべん小僧」の物理学パートツー- 風に向かって「立ちしょんべん」をするにはどうしたら良いか -を考えてみたい、と思うのである。逆風に負けずに立ちションを遂行するためにはどうすれば良いかを考えることにより、時と場所を選ばず立ちションを遂行したいと思うのである。
そこで、まずは、「立ちションベン」のパラメーターを決めてみよう。もちろん、立ちションには色々なパラメータがある。もちろん、人によっても違うだろうし、状況(観光バスの視線を集めたワタシのソレは明らかに「普通の立ちション」ではなかった…)によっても違うことだろう。しかし、ここはひとまず「しょんべん」の初速と放水を行う「銃筒」の角度を適当に決めてみる。つまり、立ちションがどの向きにどれだけの速さで放出されているかを決めてみるのである。
 「しょんべん小僧」の物理学- あともう一歩、前に出ろ - (2000.10.29) |
下左のグラフは「銃筒」を水平撃ちする歳の「しょんべん」の初速と、その場合の「しょんべん」の軌跡である。「銃筒」から「しょんべん」が秒速2,3,4mで飛び出すときの「しょんべん」の軌跡を計算してみたモノだ。縦軸が鉛直軸、横軸は立っている場所を0とした時の水平距離を示している。単位はいずれもメートルである。ショーという感じで放水中の立ちションの様子がよく判ると思う。「しょんべん」を放つ「銃筒」の高さは70cmとちょっと低めにしてしまったが、普通もう少し高い場所にあるのが自然だろう。
飛翔中のしょんべんが受けるの空気抵抗も、この計算中では考慮してあるが、この段階では未だ特に風が吹いているわけではないので、しょんべんの軌跡は大体放物線と似通っているものになっている。このグラフを眺める限りでは、しょんべんの初速は秒速3m位に設定するのが自然に思われる。場合によっては(どんな場合だ!?)、もう少し違うような感じもするのだが、とりあえず平均値としては「しょんべん」の初速は3m/s位で良いように思われる。
青 : 2m/s 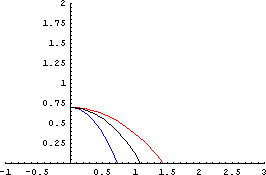 | 青 : 下向き30度 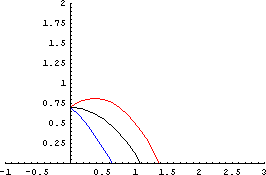 |
そして上右は試しに、「しょんべん」を放つ「銃筒」の放出角度を変えた場合の「しょんべん」の軌跡を計算してみた場合の「しょんべん」の軌跡である。ここでは下向き30度、水平撃ち、上向き30度の三種類をやってみた。この三つの場合の結果、そして色々な「しょんべん小僧」を見る限りでは、「しょんべん」の狙い方としては水平撃ちが普通だろう。自らの経験と重ね合わせてみても、「しょんべん」は水平撃ちが「安定度・飛距離」共に優れており、それ故にそのやり方が一般的ではないかと思うのである。
さて、こんな感じで大雑把に初速度を決めてみたところで、本題の風が吹いている場合の「しょんべんの軌跡」を計算してみた。下のグラフが、潮風に吹かれながら風上に向かって放水作業を行う場合の「しょんべんの軌跡」である。つまりは逆風に晒されたしょんべん小僧のしょんべんの軌跡である。
左は吹いている風の風速を0〜28m/sまで変えてみた場合のしょんべんの軌跡を計算してみたものだ。しょんべんはもちろん風上に正確に狙いを付けている。このグラフを見ると、風が強くなるに従い、しょんべんの軌跡が風に吹かれて自分の足元に吹きながされているのが判ると思う。風速3m/s位では、「しょんべんの飛びが何だかちょっとなんか違うかな?」という程度であるが、風速28m/sにもなると、自分の足元に押し戻される程度では済まず、何と自分の足先に「しょんべん爆弾」が見事に誤爆してしまっている。何とも恐ろしい事態である。秒速28m/sの風= 時速50kmの風圧と言えば、それはすなわちCカップバストの感触(擬似オッパイに関するhiraxの関係式)であるわけであるが、その「天使のCカップバスト」を装う魔の風に銃筒を向けて「しょんべん」を撃った瞬間に、何と自分の足先に天罰が下ってしまうのである。恐るべき、逆風なのだ。
黒 : 0m/s (時速0km) 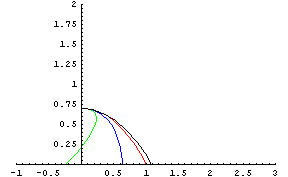 |
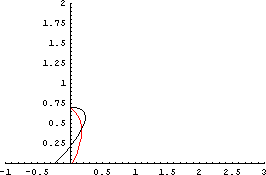 |
そこで、もちろん、そんな強風の中での立ちしょんべんをする場合に誤爆しないようにするためには、いくつかの対策がある。もちろん、誰でも思いつく一番判りやすい方法が「しょんべん」が銃筒を飛び出す初速や構える銃筒の角度を変えるというものである。風に負けない強さでしょんべんを放水したり、飛距離が出なくても良いから、風に流されにくいような銃筒の角度に狙いを変えるというものだ。右のグラフは、例えば銃筒の角度を水平撃ちを止めて、「しょんべん爆弾」が風に流されて誤爆しないように、下向き30度の速射タイプに変更してみたものである。自分の足に見事に命中していたしょんべん爆弾が、なんとか誤爆せずに地面に吸い込まれていることが判ると思う。
ところで、実は立ちションベンにはたくさんのパラメーターがある。ションベンの初速度と銃筒の角度だけではないのである。実は地味だが、大きなパラメータが数多くある。その内の一つが、しょんべんを撃つの銃筒の口径なのである。風が吹いていないような場合にはあまり関係ないが、風が強くて空気抵抗がとてもとても無視できないような場合には、この銃筒の口径は大きく効いてくるのである。空気抵抗の大きさ自体が口径の二乗で効いて、ションベンの質量は口径の三乗に比例するから、結果として口径に比例して空気抵抗の影響が小さくなる。すなわち、口径が小さいと風の影響を強く受け、口径が大きいと風の影響を受けにくいのである。つまりは、細くショワァーと放水するか、太くジョワァーと放水するかどうかはとても重要なのである。
というわけで、下のグラフが風速28mの逆風下で「しょんべんを水平に撃つの銃筒の口径」を変えてみた場合の計算結果である。口径を大きくすることで、風の影響を受けやすい水平撃ちをしているにも関わらず、しょんべん爆弾の誤爆を楽々と防ぐことができているのが判るだろう。風吹く中で立ちションを力強く安定してするためには、何より放水口の口径を大きくすることが大切なのである。
黒 : 半径 3mm 赤 : 半径 2mm (風速28/s = 55km/h下における水平撃ちの場合) 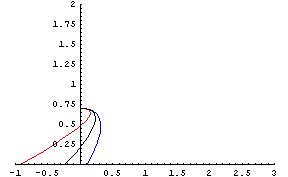 |
というわけで、「逆風に負けずに立ちションを遂行するためにはどうすれば良いか」「時と場所を選ばず立ちションを遂行するためにはどうしたら良いか」を考えてきたワタシは、「しょんべんを撃つの銃筒の口径を太くするべし」という結論を得たわけである。と、書きつつ「そんなことできるかぁー」と叫びたくもなるが、日々鍛錬をすることで、いつ日かそんなワザを拾得し、あらゆる時と場所で、雨ニモ風ニモ負ケズ、そして「天使のCカップバスト」を装う魔の風にも負けないワタシになりたい、と思うのである。
ところで、そんな「しょんべんを撃つの銃筒の口径を太くしたりする」ことが既にできるヤツラもいるのである。それはもちろん、ションベン小僧達である。だから、街中に立っているションベン小僧達、強い逆風に晒されりすることの多いションベン小僧達は、「銃筒の口径」がきっと太いのではないか、とワタシは想像するのである。なかなか、彼らのソレの口径を計ったりする機会には恵まれないのではあるが、きっと彼らは太くジョワァーと放水をすることで、風に負けない立ちション生活を貫いているのではないか、とワタシは想像したりするのである。ワタシもいつの日か、力をつけて彼ら逆風に負けないションベン小僧のようになりたいと思うのである。 …どう特訓するのか判らないけど…。
2002-09-18[n年前へ]
■銀玉鉄砲を撃ちまくれ。(前編) 
銀玉鉄砲の弾道計算
世の中には「似て非なるモノ」が溢れている。一見同じように見えるのに、よく見ると何故だか大違いというものである。そしてまた、その「似て非なるモノ」の亜種として「言葉の上ではよく似ていて、実際のところもやっっぱりよく似ているのに、世間一般での印象が全く異なるモノ」というのが数多くある。
その一例が、「月光仮面」と「けっこう仮面だ。月光仮面は「月よりの使者」をキャッチフレーズにする正義の味方で、けっこう仮面は「愛と正義の使者」をキャッチフレーズにするやはり正義の味方だ。二人ともマスクをかぶった正義の味方だし、そのキャッチフレーズだって互いによく似ているのに、世間一般の印象は大違いなのである。「昔、私は月光仮面に憧れていてね~」と遠い目で語る男を優しく見守る女性はいるかもしれないが、「なんてったって、も~、オレはけっこう仮面が好きで好きで~」と呟く男を優しく見守る女性はいるわけはないのである。同じように思い出を語っているのに、そしてその響きもほとんど同じなのに、世間の印象というのは全然違うモノなのである。「月光仮面」と「けっこう仮面」は「似て非なるモノ」なのだ。
そして、よく似た「似て非なるモノ」がもう一つある。それは銀玉と金玉である。両者ともに「金銀銅」というフレーズで並び称される「貴金属の名」に「宝石を意味する玉」が付け加えられたものであり、ギンダマという響きとキンタマという響きだってそっくりであるのに、その響きを人前で発っした場合の印象は180度違うのである。いや、実際のところはギンダマと口から発することはできたとしても、キンタマなんて口から言葉を出すことは普通一般的にはできないのである。口に出すだけでなくて、例えば恋人を部屋に呼んで、昔のおもちゃ箱を開けながら「ホラ、オレの銀玉鉄砲ー、懐かしいだろー」なんて見せびらかせば、「まだコドモみたいー、可愛いー」となるかもしれない。ところが、同じように恋人を部屋に呼んでも、「ホラ、オレの金玉鉄砲ー、スゴイだろー」なんてキンタマテッポーを見せびらかした日には、これはもう一体どうなることかわかったものではないのである。その響きも、そしてそのピストルとしての役割も、銀玉鉄砲と金玉鉄砲はよく似てはいても、その二つはやはり「似て非なるモノ」なのである。
そんな「似て非なるモノ」の片割れの「銀玉鉄砲」、生まれてはや50年ほどになる銀玉鉄砲を、昨日散歩の途中に買ってしまった。街中を歩いていると、古びたオモチャ屋が人知れずあって、その店に気づいたワタシはついつい足を踏み入れてしまったのである。そして、その店の中で棚の下の段ボールに入っていた銀玉鉄砲を見かけたワタシは、思わず銀玉鉄砲一セットを買ってしまったのである。銀玉鉄砲150円+玉100円のしめて250円ナリであった。玉は残念ながら銀玉ではなくて、BB弾だったのだけれども、少なくとも安っぽい銀玉鉄砲の方は昔と同じ見てくれだった。
「銀玉鉄砲の昔」で思い出すことといえば、子供の頃に遊んだ銀玉鉄砲を武器にした「撃ち合い遊び」だ。あの遊びのことをなんと呼んでいたのかはもう覚えていないのだけれど、きっと適当に「戦争ごっこ」とでも称していたのだったと思う。やっていることは同じでも、それを今風に「サバゲ」などと呼んでしまうとそれは「アレゲ」(=「何だか、ちょっと言い難いけど、アレっぽいよねー」という程度の曖昧な言葉)な世界になってしまう。だから、やはりここは銀玉鉄砲で「戦争ごっこ」くらいの言い方にしておくと、その「戦争ごっこ」で使われる銀玉鉄砲の射程距離は子供心にもそんなに長くなかったような気がする。確か、かなりの至近距離でバンバンと撃ち合っていたような気もするし、少なくとも狙う相手が見えないような遠くから撃つものではなかった。それに、映画の「マトリックス」の一シーンではないけれど、自分を狙って撃った弾を何とか避けたりすることも(たまには)できたりしたような気がするから、きっと銀玉はヒョロヒョロの弾道を描いていたのだと思う。
「できるかな?」では、以前「似て非なるモノ」の片割れ=金玉鉄砲の弾道計算をしたことがあった。その名前の響きも、その役割もほとんど同じ「似て非なるモノ=キンタマテッポー」の弾道計算をしたのであれば、せっかくだから今回はもう片方の「似て非なるモノ」=銀玉鉄砲の弾道計算をしてみることにしようと思う。
まず、銀玉鉄砲で発射された銀玉の初速度(≒10m/s)と、銀玉の重さ(≒0.2g)というデータと、銀玉の直径が6mm強というデータを元にまずは銀玉の弾道を計算してみた。下のグラフは「無風状態で銀玉鉄砲を1.2mの高さで水平方向に銀玉を発射してみた時の銀玉の弾道」を示している。下に示した二つのグラフの中で、上のグラフは「空気抵抗を考慮した場合」であり、下のグラフの方は「空気抵抗を考慮しない場合」である。
空気抵抗を無視すると、昔使っていた銀玉鉄砲の銀玉は7m程飛ぶことになる。しかし、実際には銀玉に空気抵抗が働くために、飛距離はそれより少しだけ短くなって6m程しか飛ばないことになる。とはいえ、空気抵抗のせいで短くなってしまった距離は高々1m程なわけで、実際のところ昔の銀玉鉄砲では空気抵抗はあまり影響していなかったのである。子供の頃の記憶を呼び起こしてみても、実際に銀玉はそんなに遠くまで飛んでいるわけではなかったし、この計算結果でも飛距離6mというと「十分遠く」まで飛んでいるとはいえなかった。だから、銀玉鉄砲のバネを改造して強くしてみたり、あるいは銀玉の重さを変えてみたりして、銀玉を遠くまで飛ばそうとした記憶がワタシにはある。その記憶に沿って、「銀玉鉄砲の銀玉の重さを変えてみた場合に銀玉の弾道がどう変わるか」を計算してみたのが下の三つのグラフである。
上のグラフを眺めてみれば、「銀玉の重さ」を軽くすると銀玉鉄砲の銀玉の飛距離はわずかながら長くなることがわかる。子供だった頃を思いおこしてみると、子供心に「銀玉の重さを軽くすると、遠くまで飛ぶハズ」という程度の曖昧な確信で改造をしていたような気がするけれど、アレは今考えてみても正しかったのだなぁ、と思うのである。もちろん、今では「銀玉鉄砲のバネのエネルギーが銀玉の運動エネルギーに変わるから、銀玉の重さの逆数のルートに比例して銀玉の初速度は速くなる。だから、空気抵抗が無視できる場合には銀玉が軽ければ遠くまで飛ぶ」と自然に考えるわけだけれど、少なくとも昔はそんなに淡々とは考えはしなかったのである。
さてさて、そんな懐かしい気分から今現在に気分を強引に取り戻して、最近巷に溢れているという強力なエアガンと昔の銀玉鉄砲の弾道を比較してみたのが下のグラフだ。昔の銀玉鉄砲より50倍ものエネルギーがある最近の強力なエアガンの場合である。そんなエアガンでは、なんと銀弾鉄砲の5倍近く25m以上もの飛距離がある。現実の兵器の世界でも性能競争が激しく行われているのと同じように、おもちゃの玩具の兵器開発も激しいようだ。5mと25mでは大違い、まさに飛び道具である。ここまでくるとやはり「玉」ではなくて「弾」と書く方がふさわしいように思えてしまう。
そして、ここまで強力になってしまうと、その特性も昔の銀玉鉄砲とは全くの別物になってしまう。その証拠に、先ほどの銀弾鉄砲の場合と同じように「発射する弾の重さを変えてみた場合の弾道」を計算してみたものを下に示してみよう。なんと、最近の強力なエアガンの場合は、弾の重さを重くすれば重くするほど遠くまで飛ぶのである。昔懐かしの銀弾鉄砲が銀玉を軽くすればするほど遠くまで飛んだのとは全く逆なのである。最近のエアガンのパワーがあまりに強力で弾の発射速度が速いために、空気抵抗による影響が支配的になってしまうのである。そのため、弾の重さが軽い割に直径が大きい弾よりも、重さの割に直径が小さい弾の方が遠くまで飛ぶようになる。
こんな風に、昔の子供のおもちゃ銀玉鉄砲と最近の強力なエアガンはパワーがあまりに違うため、結局のところその特性は「似て非なるモノ」になってしまっている。「姿形はよく似ているのに、その特質をよく見てみると少し違っていて、その印象は結構異なるモノ」になってしまっている。単にパワーの大きさが違うだけで、そんな特性・印象の違いが生まれてしまったりする。子供と大人が大きさとほんの少しの特質が違うだけで結構違う(部分もある)のと同じなのである。
そう、例えて言うなら銀玉鉄砲は「子供のおもちゃ」でエアガンは「大人のおもちゃ」なのだ。「言葉の上ではよく似ていて、実際のところもやっっぱりよく似ているのに、世間一般での印象が全く異なるモノ」になってしまっているのである。まさに、ギンダマテッポーは「子供のおもちゃ」でキンタマテッポーは「大人のおもちゃ」だったのである。そんなことを考えると、「昨日ワタシが散歩の途中に買ってしまった」のがギンダマテッポーで良かったなぁ、とつくづく思うのである。だって、「ワタシは散歩の途中に「大人のオモチャ屋」にふと足を踏み入れて、大人のおもちゃを買ってしまったのである」なんて言葉を聞く世間の印象はずいぶんと違うに違いないのだから。