2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
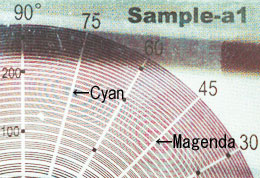
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2003-05-26[n年前へ]
■イベント・コンパニオンのヒミツ!? 
ミニか否かはハイヒール次第
世の中には「知っている人は知っている。だけど、知らない人は全然といって良いほどに知らない」というコトが数限りなくある。例えば、「スクール水着のお腹部分には大きな穴が開いている」というスクール水着のヒミツもそんなコトの一つであるし、「ミニスカートの長さは32cmを境として見える見えないの境界線が決まっている」なんていうミニスカートのヒミツもその一つであった。
知っている人には「何でいまさらそんなことを…?」と感じられるコトであっても、そのコトを知らない他の人にとってはそのコトは衝撃的以外の何ものでもなかったりするコトがある。「知っている人は知っている。だけど、知らない人は全然といって良いほどに知らない」なんていうコトほど、知っている人と知らない人の間の受け取り方のギャップが大きくなるものはないのである。
そんな「知っている人は知っている」というコトの一つがsuchi today経由で知った右の写真から判る「イベント・コンパニオンの足下のヒミツ」に違いない。
| 画像はTECHSIDE ビジネスシヨウ2003への直接リンク |
 |
まずは、そのヒミツが隠されている右の写真をよく眺めてみよう。この写真を眺めてみてももしも何も感じなかったら、あるいはこんな写真や、こんな写真、あるいは、こんな写真を立て続けに見ると判りやすいだろうか。とにかく、どの写真を見ても「あぁこれは一点透視遠近法以外の何者でもないぞ」という感じを心の中で強く受けるハズなのである。見事なぐらいに画面の奥へ奥へと直線が伸びているようすを感じるハズなのだ。
その理由はもちろん、コンパニオン達のつま先の位置も、スカートの端の位置も、視線の位置も全員が全員同じであるからだ。それはまるで、コピーして何人も複製して並べたかのように手前から奥まで全員が全員みんな同じなのである。そのせいで、コンパニオン達のつま先の位置も、スカートの端の位置も、視線の位置も、その全部が全部一直線となって画面の奥へ伸びているように見えるのである。
もちろん、現実にこれらの写真の中のコンパニオン達がみんながみんなが身長であるわけも、足の長さも同じわけであるわけもなくて、そのコンパニオン達の足下をよくよく眺めてみれば、ハイヒールの高さを調節することで背の高さを調節していることが判るに違いない。もちろん、上に挙げた他のいくつかの写真をよく眺めてみても、やはり同じようにハイヒールの高さで調節していることが判るのである。それは知ってしまえば当たり前の話で、身長が低いからといって大きい服を着せてしまえばそれはとてもヘンであるし、身長が高いからといって短いスカートを履かせたりしたら、それはもっと大ヘンな事態に陥るに違いないのである。つまり、結局のところ
「各人それぞれの本当の身長」+「各人それぞれの身長調整用ハイヒール」 = 「みんな同じ身長」となっているわけで、つまりは「金正日(キムジョンイル) ナゾの9%」と同じ身長調整システムになっているのである。コンパニオン達の股下にあるけど足じゃない、コンパニオン達の膝下にあるけど何故か足じゃない、コンパニオン達には何かヘンな部分があるという「金正日と同じ身長調整システム」なのだ。
しかし、「金正日と同じ身長調整システム」と同じということは、そのシステムを使った場合にはやたらめったら股下長さが長くなってしまうという弊害が現れるハズなのである。例えば「女性の身長v.s.股下比率」を見てみても、女性の足の長さは(身長が高い場合には比較的身長に占める股下長さが長いとはいえ)身長の 42~47%程度、つまりは身長の半分以下に過ぎない。しかし、このコンパニオン達のように身長を足下で調整してしまったりすると、その「各人それぞれの身長調整用ハイヒール」の高さが「各人の足の長さ」の中に繰り込まれてしまうのである。ということは、やたらめったら股下長さが(一見)長く見えてしまうのだ。それを言い換えるならば、そのコンパニオンの「足の長さだけがミョーに長く見えてしまう」のである。その人の体に比べてやたらに足が長く見え、そのスカートから伸びる足がやたらに長く見えてしまうのである。例えばそのコンパニオンが本当の身長にジャストフィットするようなスカートを履いていたりしたならば、その足を隠すスカートの丈が少しばかり(足に比べて)短く見えたりすることになるのである。つまり、そのコンパニオンがミニスカートを履いているように錯覚してしまったりするのである。
とはいえ、コンパニオン達にとっては「足の長さが長くなってしまう」というのは別に弊害となるわけではない。足が長く見えるのは、それはとってもウレシイ話にしか思えないハズである。それを喜びこそすれ、悲しんだりするわけはないのだ。むしろ、その悲劇は一見無関係に思えるワタシ達傍観者の側に訪れるのだ。なぜなら、それらのコンパニオンに見とれるワタシ達は
- スカートから伸びる足がやたらに長く見え、スカートの丈が足の長さに比べて短いぞ、と気づく
- ということは、アレは結構なミニスカートだなと考えて(実は勘違い)、も・もしかして見えるかも… 、と期待をする
- しかし、実際にはそのスカートが短いわけではないので(それにワタシ達は気づくこともなく)、無駄な時間を過ごしてしまう…
しかし、「コンパニオン達が身長を足下で調整している」という簡単で「知っている人は知っている」事実を知っしまえば、実はコンパニオン達が「金正日と同じ身長調整システム」を採用しているという「イベント・コンパニオンの足下のヒミツ」を知りさえすれば、もう金輪際ワタシ達がこんな悲劇的なシチュエーションに陥ることはないのである。例えば、無垢なワタシ達がもしも何かのイベントに行ったとしても、まずは即座にコンパニオンの足下を確認し、「そのハイヒールがずいぶんと厚底である」と確認したならば、哀しげに首を振りながら「あのスカートは短く見えるけれどそれは目の錯覚で、本当は特に短くもないただのスカートなのだ」と自分を静かに納得させることができるようになるのである。そしてさらには、コンパニオン達の足下を見渡して、ハイヒールの「かさ上げ」がほとんどないコンパニオンを見つけたならば、「このコンパニオンのスカートは(短くは見えないけれど)本当は短いのだ」と心の中で喜びつつ、満足感と期待感とともにそのスカートに見とれることができるようになるのである。
というわけで、イベントに行ったならばコンパニオンの足下をまずは確認すべし、そして低いハイヒール(という言い方もヘンだが)のコンパニオンを見つけてそのスカートに見とれるべし、というのが今回の「必ずトクする今日の一言」なのである。いや、ホントのところはどうだか知らないのだけれど…。
2003-06-17[n年前へ]
■アルキメデスのパンチラの式 
「スカート円錐」の明るさを探れ
「スカート円錐」の明るさを探れ
以前、「ミニスカートの幾何学」として、女子高生の間などで流行っていたミニスカートの丈の短さの限界について考えてみたことがある。階段を上ろうとしているミニスカートを履いた女性(別に男性でも構わないが…)の下着が見えてしまうかあるいは見えないのかを、女性達が履くミニスカートの丈の長さから考察をしてみたのであった。その「ミニスカートの幾何学」の考察をした結果、ミニスカートの丈がちょうど32cmの時に、ミニスカートで下着が隠されはじめる境界線がちょうど階段と平行になる、ということが判ったのである。そして「下着が隠されはじめる境界線がちょうど階段と平行になる」結果、ミニスカートの丈が32cmより短いと下着が階段下を上る人達から見えてしまうようになり、逆にミニスカートが32cm以上の丈であればスカートの中の下着はなんと幸か不幸か見えることはないのだ、ということが判ったのである。ミニスカートをはいた女子高生が急な駅の階段なんかを上るときでも、ミニスカートの丈が32cm以上であれば、パンチラの恐怖に怯える必要はないということが判ったのであった。
ところで、ミニスカートの中が見えてしまいそうになる場所というのは、必ずしも急な階段だけではないらしい。最近の東京の有名スポットなどでは、「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかがたくさんあったりするというのである。そして、そんな場所では、真上にいる「スカートを履いた女性」を急角度で仰ぎ見ることができて、スカートの中の下着がチラリと見えてしまうことがあるというのである。
しかし、である。角度的にスカートの中の下着が見えるからといって、果たして本当に下着が見えるものなのだろうか?角度的には見えるはずでも、実際には人間の目には見えないことだってあるのではないだろうか。なぜなら、スカートが「私たちの視線から下着が見えるのを遮っている」のと同じように、スカートは「照明の光が下着にあたるのをも遮っている」のである。スカートの中というのはスカートに光が遮られて(たぶん)かなり暗いハズなのである。いや、実際に覗いてみた経験があるわけでは決してないので自信を持って「ハズ」と断言することはできないのだけれど、スカートの中が明るいわけはないと思うのである。もし、スカートの中が明るくなければ、仮にその中身を覗くことはできても結局暗くて何も見えないわけで、「スカートの中が(見えるくらいに)十分に明るいかどうか」が肝心だと思うのである。そこで、今回は「下着が角度的に見通せる条件」ではなくて、「スカートの中の下着が十分明るく見える条件」を考えてみたい。
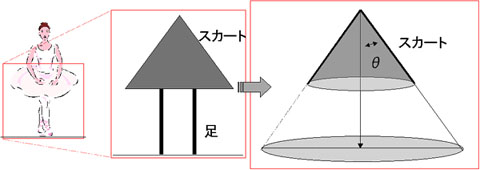
まずは、スカートをはいた女性を下の図のように簡単に示してみよう。スカートを下向きに開いた円錐として考えてみる。もちろん、スカートの中の下着はこの円錐の頂点に位置するわけだ。そして、スカートが広がる角度をΘとでもしてみることにしよう。その時、円錐の頂点にはどれだけの光が当たるものだろうか?
 |
もちろん、円錐状のスカートが上からの光は遮っているわけだから、スカートの中の下着を照らす光というのは、下の床からの反射光だけである。つまりは、上の図で、「色を付けた部分の床」からの反射光のみが下着にまでたどり着き、それ以外の床からの反射光はスカートに遮られて、スカートの中を照らすことはない。ということは、「スカートの中はどれくらい明るいか?」という疑問を考えることは、それは「色を付けた部分の床からスカートの中の下着にまでたどり着く光がどれだけあるか?」ということを考えることと同じなのである。
そしてまた、床上での光の反射に方向性が無く、光が完全に等方的に周囲に拡散するとするならば、円錐の中心(つまりはスカートの中の下着部分だ)にあたる光の量は、下の左図の色を付けた部分球の面積に比例する。つまり、「スカートの中の明るさ」は「スカートの広がり角」で決められる「部分球」の面積に比例するのである。
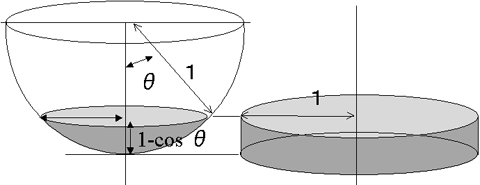 |
つまり、角度Θで広がるスカートの中が「どれくらい明るいか?」という疑問は、「下図で色を付けた部分球の面積はどのくらいか?」という問題に変わるわけである。「半球全体の面積に対して、スカートの広がりで決められる部分球の面積はどのくらいの割合か?」ということの答えが、それすなわち「スカートの中の明るさ」を決めているのである。
ところで、アルキメデスが発見したように、球(もしくはその一部)の面積はその球に外接する円筒の面積に等しい。つまり、上の図の左で色を付けた部分の面積というのは、右に示したような(色を付けた)円筒の面積に等しいわけだ。ということは、右の円筒部分の面積は
円筒の面積 = 2 π (1-cosΘ)であって、左の半球の面積が(直径=1とすると)2πだから、円錐状のスカートの中の明るさは、スカートの広がる角度をΘとするならば、「スカートの中の明るさ」は
という実に簡単な式で表されることになる。アルキメデスも、まさか自分の球と円筒の表面積に関する発見が「スカートの中の明るさを示す式(ここでは仮に『パンチラの式』とでも呼ぶことにする)」を導くために使われるとは想像だにしなかっただろうと思うが、とにかくアルキメデスのおかげで私たちはスカートの中の明るさを知ることができるのである。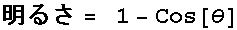
試しに、このくアルキメデスの『パンチラの式』を使って、スカートの広がり角度Θに対して、スカートの中の明るさがどのように変化するかを計算してみると、その結果は下のグラフのようになる。このグラフは、横軸が「スカートの広がる角度」で、縦軸が「スカートの中の明るさ」を示している。周囲の「照明に照らされている床」の明るさを1とした時の「スカートの中の明るさ」を示しているのである。
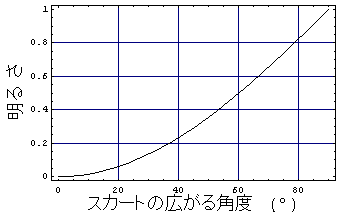 |
基本的にはスカートが広がるにつれて「スカートの中の明るさ」は明るくなるわけであるが、このグラフを眺めてみると、スカートの広がる角度が20°を超えるあたりから次第にスカートの中が明るくなることが判るだろう。例えば、スカートの広がる角度が30°の時には、スカートの中は「床の明るさの10%程度の明るさ」しかないが、スカートの広がる角度が60°にまで広がれば、スカートの中は「床の明るさの半分程度の明るさ」になる、ということが判るわけだ。
ところで、人間の目というものは「見るものの明るさ」に合わせて順応する。例えば、暗いものを見るときには目の感度は自動的に上がる。だから、スカートの中がほのかでも明るかったならば(例えば床の明るさの5%程度にでも明るければ)、自動的にその明るさに目が順応してスカートの中が見えてしまうかと思いきやそうはいかない(ハズだ)。なぜなら、人間の目は明るいものを見る時には、目の感度が逆に自動的に低下してしまうからである。スカートの中以外の明るい場所(例えば照明や、照明に照らされた明るい壁)だって、自動的に視界の中に入ってくるわけで、目の感度はそういう明るい部分に自動的に合ってしまうハズなのである。
例えば、下の画像は周りの明るさに対して、
- 5%の明るさ
- 10%の明るさ
- 20%の明るさ
| 5 % | 10 % | 20 % |
ということは、先のグラフで「スカートの中の明るさ」が10%を超えていないと、つまりは周囲にある明るい床(や照明や壁)などの明るさの10%を超えているくらいでないと、スカートの中が仮に幾何学配置的に見える条件であったとしても、実際には目の感度的にその中のようすを判別することができないに違いないのである。その場合、おそらく明るい床や壁の明るさに目の感度が合ってしまい、ほの暗いはずのスカートの中は真っ暗にしか見えず、幸か不幸かスカートの中身は識別することができないハズなのだ。
というわけで、先ほどのグラフに「識別できる明るさか否か」を書き入れてみると、次のグラフのようになる。
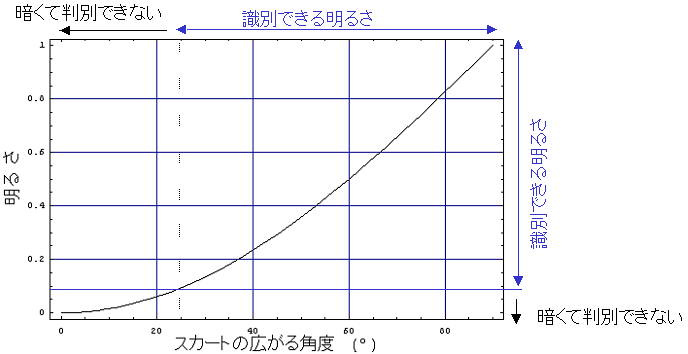 |
つまり、スカートの広がる角度が25-30°を超えていないと、スカートの中身は周囲の床や壁の明るさに比べて相対的に暗すぎて人間の目ではおそらく見ることができないのだ。
例えば、スカートの広がる角度が30°以下に制限されるようなタイトスカートを穿いて、明るい壁や照明などが視界にどうしても入ってしまうような場所にたたずんでいる限りは、もし仮にスカートの中を覗かれたとしてもスカートの中は(人間の目からすると)真っ暗で何も見えないわけで、スカートの中身を見られたりするような被害にあうことはまずないだろう、ということが先のアルキメデスの『パンチラの式』から判るわけなのである。「吹き抜け構造の建物内で階下から階上を見上げられる場所」や「建物内外の渡り廊下を見上げられる場所」なんかであったとしても、背後に明るく輝くものがある限りには、見る人の目を眩ませることができて、スカートの中身は安全なわけである。
ところが逆に、床が白かったりして明るいクセ(つまり下からの照明が強いクセ)に、周りに明るい壁や照明が何故かあまりないような場所がもしあったとして、もしそんな場所で(下から)スカートの中を覗かれたりしてしまうと、(下から覗く人の視界に入る)周囲の明るさに比べてスカートの中が十分明るく見えるせいで、しっかりとパンツの模様をチェックされてしまうということになるだろう、ということも予想することができてしまうのである。だから、そんな場所をもしも短いスカートをはいて歩かなければならないような場合には、例えば何かの「ピッカピッカ輝く光りモノ」でも身につけて、その光りモノの明るさを「スカートの中身をのぞこうとするスナイパー」の視界に入れて、彼らの目を眩ませてしまえば良いだろう、というアルキメデスの知恵さえ授けてくれるのだ。
ところで、今回は「スカートの中の明るさを示す=パンチラの式」を考えてみたわけであるが、この式は考えるまでもなく実にアブナイ式である。パンチラの被害防止に役に立ちそうな気もするし(全然役に立たないような気もするが)、逆に単なる「パンチラの科学」になってしまっているような気もしてしまう。「スカートの中身をのぞこうとするスナイパー」の魔の手から逃げるためのバイブルになるような気もするし、「スナイパー」のための手引き書になってしまいそうな気もする。ギリシャ神話で、あらゆる災厄が入っていたという箱がパンドラの箱だったけれど、このパンチラの式だって案外そんなパンドラの箱のような、色んな災厄の元になってしまうものかもしれないのである。しかも、パンドラの箱の場合には最後に箱の中に『希望』が残っていたわけでまだ良い(?)のである。しかし、アルキメデスの『パンチラの式』の場合には「スカートの中にだっては『希望』が入っているのだぁ」などと口に出したりしたら単に変態扱いされてしまうだけなわけで、そこはパンドラの箱よりもずっとたちが悪いのである。つまりは、科学もアルキメデスの『パンチラの式』も使う人次第なのである。
2003-06-21[n年前へ]
■文の長さは女性のミニスカート 
今日見た素晴らしい名言。
Sentence length is like a girl's skirt:the shorter the better, but it should cover the most important parts. 文の長さは女性のミニスカートのようなもので、短ければ短いほど良い。しかし、最も大切な部分はカバーしていなければならない。
2003-10-05[n年前へ]
■ミニスカートは男の視線を強制的に集める 
面白い考察。 from PSYCHO-MYU。
